قاعدة sin
ما هو قانون sin
قاعدة الجيب (Sin) هي إحدى الوظائف الرياضية الأساسية، وتمثل النسبة بين طول الضلع المقابل لزاوية معينة في المثلث القائم إلى طول الوتر (الضلع المقابل للزاوية القائم). إذا كانت θ هي الزاوية المقابلة للضلع، وc هو طول الوتر، و a هو الضلع المقابل للزاوية، فإن قاعدة الجيب تُعرَف كالتالي:
a/c =(sin(θ
حيث:
- (sin) (θ ) sin(θ) هو جيب الزاوية
- θ. a هو طول الضلع المقابل للزاوية
- θ. c هو طول الوتر (الوتر يعني الضلع المقابل للزاوية القائم).
هذه القاعدة تستخدم على نطاق واسع في حسابات المثلثات والزوايا في الرياضيات والفيزياء. يمكن استخدام الأجهزة الحاسبة العلمية لحساب قيم الجيب لزوايا مختلفة.
قاعدة sin
تتراوح قيم الجيب بين -1 و1، حيث يكون القيمة 1 عندما تكون الزاوية مقدارها 90 درجة (المثلث القائم)، وتكون القيمة 0 عندما تكون الزاوية مقدارها 0 درجة، وتكون -1 عندما تكون الزاوية مقدارها 180 درجة.
على سبيل المثال:
- إذا كانت لديك زاوية θ تساوي 30 درجة في مثلث قائم، وكانت الضلع المقابل لها (a) يساوي 1 والوتر (c) يساوي 2، يمكنك حساب قيمة الجيب كالتالي:
- sin ( 3 0 ∘ ) = 1 2 sin(30 ∘ )= 2 /1
- لذا، sin ( 3 0 ∘ ) = 0.5 sin(30 ∘ )=0.5.
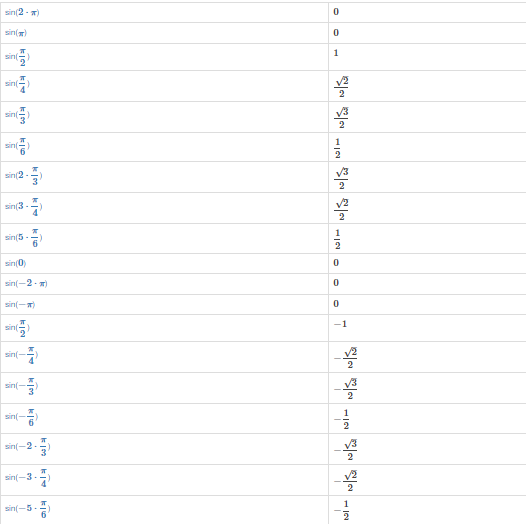
كيف يُستخدم قانون sin
الجيب (sin) يُستخدم في مجموعة واسعة من المجالات في الرياضيات والفيزياء والهندسة. إليك بعض الاستخدامات الشائعة للجيب:
- حساب الزوايا في المثلثات: يُستخدم الجيب لحساب زوايا المثلثات القائمة. عند معرفة قيمة جيب الزاوية، يمكنك حساب الزاوية نفسها باستخدام دالة الجيب العكسية (arcsin أو sin^(-1)).
- حساب الإحداثيات في نظام الإحداثيات القطبية: في النظام الإحداثيات القطبية، يُمكن استخدام الجيب لتحويل الإحداثيات بين الشكل القطبي والشكل المستطيل.
- الاستخدام في الهندسة الفيزيائية: يستخدم الجيب في حساب القوى والتسارعات والحركة الدورانية.
- الاستخدام في مجالات الكهرباء والمغناطيسية: يستخدم الجيب في تمثيل الموجات الكهرومغناطيسية والتيار المتردد.
- الاستخدام في الرسم البياني والإحصاء: يُستخدم الجيب في إنشاء الرسوم البيانية وتحليل البيانات.
- تحليل الحركة الدورانية: يُستخدم الجيب في دراسة الحركة الدورانية للأجسام والتفاعلات الفيزيائية ذات الدوران.
- في علم الصوت والموسيقى: يستخدم الجيب في فهم موجات الصوت والترددات الموسيقية.
- في البرمجة وتطوير البرمجيات: يمكن استخدام دوال الجيب في البرمجة لحساب قيم الجيب في تطبيقات الرسوم البيانية والمحاكاة.
هذه فقط بعض الاستخدامات الشائعة، ويمكن العثور على الجيب في العديد من المفاهيم والتطبيقات في مجالات متعددة.
أهمية قانون sin في الرياضيات
قانون الجيب (sin) له أهمية كبيرة في الرياضيات والعلوم بشكل عام، وذلك للعديد من الأسباب:
- حل المثلثات: في هندسة المثلثات، يلعب الجيب دورًا حاسمًا في حساب الزوايا والأضلاع في المثلثات، خاصة في المثلثات القائمة. يمكن استخدام الجيب لحساب الأضلاع أو الزوايا عند معرفة بعض المتغيرات الأخرى.
- نظرية الموجات والفيزياء: يتم استخدام الجيب في تحليل الموجات، حيث يمكن استخدامه لتمثيل الحركة الدورانية أو الاهتزازية للأشياء، مثل الموجات الصوتية أو الموجات الكهرومغناطيسية.
- تحويل الإحداثيات: يُستخدم الجيب في تحويل الإحداثيات بين النظام الإحداثي المستطيلي والنظام الإحداثي القطبي، مما يسهل تحليل الأشكال الهندسية بشكل أكثر فعالية.
- الرياضيات العليا والتحليل الرياضي: يظهر الجيب بشكل كبير في مواضيع الرياضيات العليا والتحليل الرياضي، مثل تمثيل الدوال الجيبية باستخدام سلاسل تراكمية (مثل سلسلة تايلور).
- التفاضل والتكامل: يُستخدم الجيب في العديد من التفاضلات والتكاملات، حيث تكون مشتقة الجيب جزءًا من العديد من الدوال التي تظهر في الرياضيات التفاضلية.
- علم الإحصاء: يمكن استخدام الجيب في علم الإحصاء لتحليل البيانات وتقديم النتائج بشكل إحصائي.
- البرمجة والحوسبة: يُستخدم الجيب في البرمجة لحساب القيم الزاوية والرياضية في التطبيقات والألعاب والبرامج الحاسوبية.
فهم الجيب وكيفية استخدامه يعتبر أمرًا أساسيًا في دراسة الرياضيات والعلوم، ويسهم في فهم الظواهر الطبيعية وتحليل النماذج الرياضية.
متي نستخدم ال sin
تُستخدم الجيب (sin) في العديد من السياقات والتطبيقات. إليك بعض الحالات الشائعة التي يتم فيها استخدام الجيب:
- حساب الزوايا والأضلاع في المثلثات: عند توفر معلومات حول زاوية واحدة والضلع المقابل لها في مثلث قائم، يمكن استخدام الجيب لحساب الزوايا أو الأضلاع الأخرى.
- تحليل الحركة الدورانية: يستخدم الجيب في دراسة الحركة الدورانية للأجسام، سواء كان ذلك في الفيزياء الكلاسيكية أو في الفيزياء الحديثة.
- تمثيل الموجات: يُستخدم الجيب لتمثيل الموجات الرياضية، سواء كانت موجات صوتية أو موجات كهرومغناطيسية.
- الهندسة الإحصائية والاحتمالات: يمكن استخدام الجيب في حساب الاحتمالات والتوزيعات الإحصائية.
- الحوسبة العلمية والبرمجة: يُستخدم الجيب في البرمجة لحساب القيم الرياضية، ويكون له دور في العديد من التطبيقات في الحوسبة العلمية.
- الأمور الهندسية الأخرى: في الهندسة، يمكن استخدام الجيب لحل العديد من المسائل ذات الطابع الهندسي والفيزيائي.
- تحويل الإحداثيات: يُستخدم الجيب في تحويل الإحداثيات بين النظام الإحداثي المستطيلي والنظام الإحداثي القطبي.
- تحليل السلوك الدوري: في الرياضيات، يستخدم الجيب في تحليل السلوك الدوري للدوال والتنقل بين القمم والأوجه.
هذه بعض الأمثلة، وهناك العديد من السياقات الأخرى حيث يمكن استخدام الجيب في الرياضيات والعلوم. يعتبر فهم كيفية استخدام الجيب مهمًا لفهم مفاهيم أوسع في هذه المجالات.
من مبتكر قانون sin
الدوال الجيبية (مثل السين) ومفهومها كانت موجودة في الرياضيات القديمة، وليس لدي معلومات دقيقة حول من كان أول من اكتشفها أو استخدامها. ومع ذلك، يمكننا القول أن الرياضياتيين القدماء في مختلف الحضارات كانوا يعملون على تطوير الرياضيات واكتشاف مفاهيمها، بما في ذلك الدوال الجيبية.
على سبيل المثال:
- الرياضياتي الهندي بينولاهيتا يعود إليه الفضل في تقديم بعض الأفكار حول الجيب والدوال المثلثية في القرن السابع الميلادي.
- في العصور الوسطى، زادت الدراسات حول الجيب في العالم الإسلامي، ومن بين العلماء الذين قدموا إسهامات في هذا المجال كان الرياضي والفيلسوف الإسلامي البيروني (أبو ريحان البيروني).
- في العصور الأكثر حداثة، عمل العديد من الرياضيين والعلماء على تطوير فهمنا للدوال الجيبية، ومن بينهم الرياضيين الأوروبيين مثل ليونهارد أويلر وكارل فريدريش غاوس.
تطوير الرياضيات كانت عملية تطور تاريخية حيث ساهم العديد من العلماء في تطوير المفاهيم والأفكار على مر العصور.
ال sin في حساب المثلثات
الجيب ( sin) هو وظيفة رياضية تستخدم في حساب المثلثات، وبشكل خاص في المثلثات القائمة. المثلث القائم هو مثلث يحتوي على زاوية قائمة، وهي زاوية تساوي 90 درجة. في المثلث القائم، يكون الوتر (الضلع المقابل للزاوية القائمة) واحداً من الأضلاع، والجيب ( sin sin) له دور مهم في حساب الطول الأفقي (الضلع المقابل للزاوية التي نحسب لها الجيب).
لنفترض أن لدينا مثلثًا قائمًا ABC حيث زاوية B هي الزاوية القائمة. يكون c هو الوتر (الضلع المقابل للزاوية القائمة)، وa وb هما الأضلاع الأخرى.
يُمكن استخدام القاعدة أيضًا لحساب الزوايا إذا كانت معروفة الطول الأفقي والوتر. تكمن أهمية هذه العلاقة في تيسير حسابات الطول والزوايا في المثلثات القائمة والتي تظهر في العديد من المجالات مثل الهندسة والفيزياء.
